Задача
Дан выпуклый четырехугольник ABCD. Лучи ABи CDпересекаются в точке P, а лучи BCи AD — в точке Q. Докажите, что четырехугольник ABCDописанный тогда и только тогда, когда выполняется одно из следующих условий: AB+CD=BC+AD,AP+CQ=AQ+CPили BP+BQ=DP+DQ.
Решение
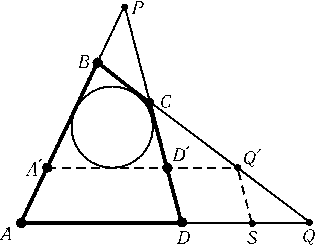
Докажем сначала, что если четырехугольник ABCDописанный, то выполняются все условия. Пусть K,L,Mи N — точки касания вписанной окружности со сторонами AB,BC,CDи DA. Тогда AB+CD=AK+BK+CM+DM=AN+BL+CL+DN=BC+AD,AP+CQ=AK+PK+QL-CL=AN+PM+QN-CM=AQ+CPи BP+BQ=AP-AB+BC+CQ= (AP+CQ) + (BC-AB) =AQ+CP+CD-AD=DP+DQ. Докажем теперь, например, что если BP+BQ=DP+DQ, то четырехугольник ABCDописанный. Рассмотрим для этого окружность, касающуюся стороны BCи лучей BAи CD. Предположим, что прямая ADне касается этой окружности; сдвинем эту прямую так, чтобы она коснулась окружности (рис.). Пусть S — такая точка прямой AQ, что Q'S|DD'. Так как BP+BQ=DP+DQи BP+BQ'=D'P+D'Q', то QS+SQ'=QQ'. Получено противоречие. В двух других случаях доказательство проводится аналогично.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь