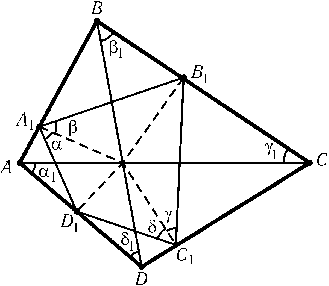
Воспользуемся обозначениями рис. Условие вписанности четырехугольника A₁B₁C₁D₁эквивалентно тому, что ($\alpha$+$\beta$) + ($\gamma$+$\delta$) = 180^o, а перпендикулярность диагоналей ACи BD — тому, что ($\alpha_{1}^{}$+$\delta_{1}$) + ($\beta_{1}^{}$+$\gamma_{1}^{}$) = 180^o. Ясно также, что $\alpha$=$\alpha_{1}^{}$,$\beta$=$\beta_{1}^{}$,$\gamma$=$\gamma_{1}^{}$и $\delta$=$\delta_{1}$.

Ответ задачи отсутствует