Задача
На сторонах AB, BC, CD и DA квадрата ABCD построены внутренним образом правильные треугольники ABK, BCL, CDM и DAN. Докажите, что середины сторон этих треугольников (не являющихся сторонами квадрата) и середины отрезков KL, LM, MN и NK образуют правильный двенадцатиугольник.
Решение
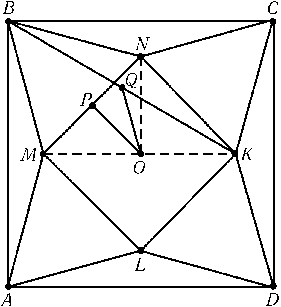
Треугольник BMC равнобедренный с углом при вершине 30° и углом при основании 75°. Следовательно, треугольники BAM и BCN равнобедренные с углом 15° при основании. Поэтому треугольник BMN правильный. Пусть O – центр квадрата, P и Q – середины отрезков MN и BK (см. рис.). Так как OQ – средняя линия треугольника MBK, то OQ = 1/2 BM = MP = OP и ∠QON = ∠MBA = 15°, а значит, ∠POQ = ∠PON – ∠QON = 30°.
Дальнейшее доказательство проводится аналогично.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь