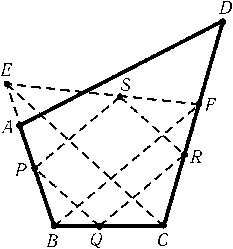
Возьмём на прямых AB и CD точки E и F так, чтобы прямые BF и CE имели заданные направления. Рассмотрим всевозможные параллелограммы PQRS с заданными направлениями сторон, вершины P и R которых лежат на лучах BA и CD, а вершина Q – на стороне BC (см. рис.). Докажем, что геометрическим местом вершин S является отрезок EF.

  В самом деле,  SR:EC = PQ:EC = BQ:BC = FR:FC,  то есть точкаSлежит на отрезкеEF. Обратно, если точкаSлежит на отрезкеEF, то проведём  SP || BF,  PQ || EC  и  QR || BF  (P, Q, R– точки на прямыхAB, BC, CD). Тогда  SP:BF = PE:BE = QC:BC = QR:BF,  то есть  SP = QR  иPQRS– параллелограмм.   Из этого вытекает следующее построение. Строим сначала точкиEиF. ВершинаSявляется точкой пересечения отрезковADиEF. Дальнейшее построение очевидно.

Ответ задачи отсутствует