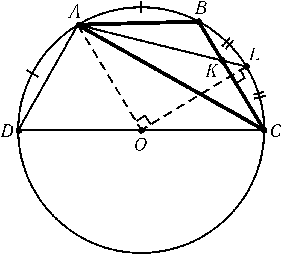
Предположим, что треугольник ABCпостроен. Проведем диаметр CDописанной окружности. Пусть O — центр описанной окружности, L — точка пересечения продолжения биссектрисы AKс описанной окружностью (рис.). Так как $\angle$ABC-$\angle$ACB= 90^o, то $\angle$ABD=$\angle$ACB; поэтому $\smile$DA=$\smile$AB. Ясно также, что $\smile$BL=$\smile$LC. Следовательно, $\angle$AOL= 90^o. Из этого вытекает следующее построение. Строим окружность Sс центром Oи данным радиусом. На окружности Sвыбираем произвольную точку A. Строим точку Lна окружности Sтак, что $\angle$AOL= 90^o. На отрезке ALстроим отрезок AK, равный данной биссектрисе. Через точку Kпроводим прямую l, перпендикулярную OL. Точки пересечения прямой lс окружностью Sявляются вершинами Bи Cискомого треугольника ABC.

Ответ задачи отсутствует