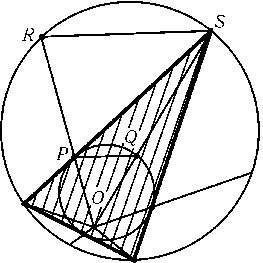
Пусть O — центр гомотетии, переводящей вписанную окружность в описанную. Разобьем плоскость лучами, выходящими из точки Oи проходящими через вершины многоугольника и точки касания его сторон с вписанной окружностью (рис.). Достаточно доказать требуемое неравенство для частей кругов и многоугольника, заключенных внутри каждого из образованных этими лучами углов. Пусть стороны угла пересекают вписанную и описанную окружности в точках P,Qи R,Sсоответственно, причем P — точка касания, а S — вершина многоугольника. Площади частей кругов больше площадей треугольников OPQи ORS, поэтому достаточно доказать, что 2S_OPS$\leq$S_OPQ+S_ORS. Так как 2S_OPS= 2S_OPQ+ 2S_PQSи S_ORS=S_OPQ+S_PQS+S_PRS, остается доказать, что S_PQS$\leq$S_PRS. Это неравенство очевидно, так как высоты треугольников PQSи PRS, опущенные на основания PQи RS, равны, a PQ<RS.

Ответ задачи отсутствует