Задача
Докажите, что площадь параллелограмма, лежащего внутри треугольника, не превосходит половины площади треугольника.
Решение
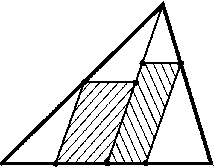
Рассмотрим сначала случай, когда две стороны параллелограмма лежат на прямых ABи AC, а четвертая вершина Xлежит на стороне BC. Если BX:CX=x: (1 -x), то отношение площади параллелограмма к площади треугольника равно 2x(1 -x)$\leq$1/2. В общем случае проведем параллельные прямые, содержащие пару сторон данного параллелограмма (рис.). Площадь данного параллелограмма не превосходит суммы площадей заштрихованных параллелограммов, а они относятся к разобранному выше случаю. Если прямые, содержащие пару сторон данного параллелограмма, пересекают лишь две стороны треугольника, то можно ограничиться одним заштрихованным параллелограммом.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь