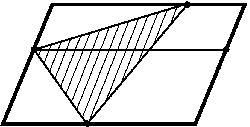
Рассмотрим сначала такой случай: две вершины Aи Bтреугольника ABCлежат на одной стороне PQпараллелограмма. Тогда AB$\leq$PQи высота, опущенная на сторону AB, не больше высоты параллелограмма. Поэтому площадь треугольника ABCне больше половины площади параллелограмма. Если же вершины треугольника лежат на разных сторонах параллелограмма, то две из них лежат на противоположных сторонах. Проведем через третью вершину треугольника прямую, параллельную этим сторонам (рис.). Она разрезает параллелограмм на два параллелограмма, а треугольник — на два треугольника, причем у обоих треугольников две вершины лежат на сторонах параллелограмма. Приходим к рассмотренному случаю.

Ответ задачи отсутствует