Задача
В некотором лесу расстояние между каждыми двумя деревьями не превосходит разности их высот. Все деревья имеют высоту меньше 100 м.
Докажите, что этот лес можно огородить забором длиной 200 м.
Решение
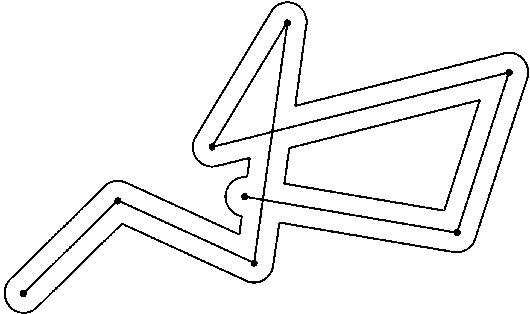
Пусть деревья высотой a1 > a2 > ... > an растут в точках A1, ..., An. Тогда по условию A1A2 ≤ a1 – a2, ..., An–1An ≤ an–1 – an. Следовательно, длина ломаной A1A2...An не превосходит (a1 – a2) + (a2 – a3) + ... + (an–1 – an) = a1 – an < 100 м. Эту ломаную можно огородить забором, длина которого не превосходит 200 м (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет