Задача
Пустьa,b,cиa',b',c'— длины сторон треугольниковABCиA'B'C',SиS'— их площади. Докажите, что
a2(- a'2 + b'2 + c'2) + b2(a'2 - b'2 + c'2) + c2(a'2 + b'2 - c'2)$\displaystyle \ge$16SS',
причём равенство достигается тогда и только тогда, когда эти треугольники
подобны (Пидо).
Решение
Построим на сторонеBCтреугольникаABCвнутренним образом треугольникA''BC, подобный треугольникуA'B'C'. При этомA''A= 0 тогда и только тогда, когда треугольникиABCиA'B'C'подобны. По теореме косинусов
| A''A2 | = AC2 + A''C2 - 2AC . A''C cos(C - C') = | |
| = b2 + |
Поэтому
| a'2A''A2 | = b2a'2 - a2b'2 - 2aa'bb'cos C cos C' - 2aa'bb'sin C sin C' = | |
| = b2a'2 - a2b'2 - 2aa'bb'cos C cos C' - 8SS'. |
Следовательно,b2a'2-a2b'2- 2aa'bb'cos Ccos C'$\ge$8SS', т.е.
b2a'2 - a2b'2 - 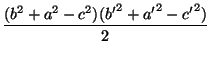 $\displaystyle \ge$8SS'.
$\displaystyle \ge$8SS'.
Это неравенство легко приводится к требуемому виду.
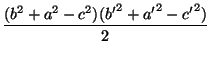 $\displaystyle \ge$8SS'.
$\displaystyle \ge$8SS'.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет