Задача
Пусть K,L,Mи N — середины сторонAB,BC,CDи DAвыпуклого четырехугольникаABCD. а) Докажите, чтоKM$\le$(BC+AD)/2, причем равенство достигается, только еслиBC|AD. б) При фиксированных длинах сторон четырехугольникаABCDнайдите максимальные значения длин отрезковKMи LN.
Решение
а) Достроим треугольникCBDдо параллелограммаCBDE. Тогда2KM=AE$\le$AD+DE=AD+BC, причем равенство достигается, только еслиAD|BC. б) Пустьa=AB,b=BC,c=CDи d=DA. Если|a-c| = |b-d|$\ne$0, то согласно задаче а) максимум достигается в вырожденном случае, когда все точки A,B,Cи Dокажутся на одной прямой. Предположим теперь, например, что|a-c| < |b-d|. Достроим треугольникиABLи LCDдо параллелограммовABLPи LCDQ. ТогдаPQ$\ge$|b-d|, а значит,LN2= (2LP2+ 2LQ2-PQ2)/4$\le$(2(a2+c2) - (b-d)2)/4. Кроме того, согласно задаче a)KM$\le$(b+d)/2. Оба равенства достигаются, когдаABCD — трапеция с основаниямиADи BC. Построим окружность S, касающуюся стороныABи лучейBCи AD, и перенесем треугольникCNDпараллельно (в направлении основанийBCи AD) так, чтобы точка N'совпала с точкой M, т. е. сторонаC'D'касалась окружности S(рис.).
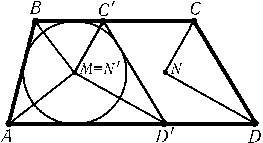
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь