Возможны два случая:

1. Точка Pлежит на некоторой диагоналиAB. Тогда прямыеPAи PBсовпадают и не пересекают сторон. Остаются 2n- 2 прямые; они пересекают не более 2n- 2 сторон.
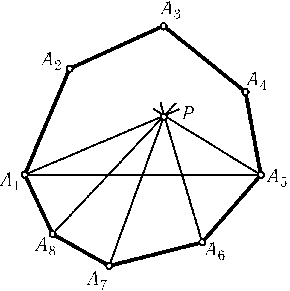
2. Точка Pне лежит на диагонали многоугольникаA₁A₂...A_2n. Проведем диагональA₁A_{n + 1}. По обе стороны от нее лежит по nсторон. Пусть для определенности точка Pлежит внутри многоугольникаA₁...A_{n + 1}(рис.). Тогда прямыеPA_{n + 1},PA_{n + 2},...,PA_2n,PA₁(число этих прямых равноn+ 1) не могут пересекать стороныA_{n + 1}A_{n + 2},A_{n + 2}A_{n + 3},...,A_2nA₁. Поэтому оставшиеся прямые могут пересекать не более чемn- 1 из этих nсторон.

Ответ задачи отсутствует