Задача
На плоскости дано пять точек, причем никакие три из них не лежат на одной прямой. Докажите, что четыре из этих точек расположены в вершинах выпуклого четырехугольника.
Решение
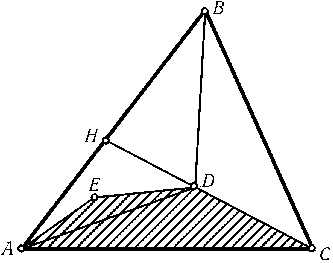
Рассмотрим выпуклую оболочку данных точек. Если она является четырех- или пятиугольником, то все ясно. Допустим теперь, что выпуклая оболочка является треугольникомABC, а точки Dи Eлежат внутри его. Точка Eлежит внутри одного из треугольниковABD,BCD,CAD; пусть для определенности она лежит внутри треугольникаABD. Обозначим точку пересечения прямыхCDи ABчерез H. Точка Eлежит внутри одного из треугольниковADHи BDH. Если, например,Eлежит внутри треугольникаADH, тоAEDC — выпуклый четырехугольник (рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь