Докажем сначала, что если Aи B — соседние вершиныn-угольника, то из Aили из Bможно провести диагональ. Случай, когда внутренний угол многоугольника при вершине Aбольше180^o, разобран в решении задачи 22.20, а). Предположим теперь, что угол при вершине Aменьше180^o. Пусть Bи C — вершины, соседние с A. Если внутри треугольникаABCнет других вершин многоугольника, тоBC — диагональ, а если P — ближайшая к Aвершина многоугольника, лежащая внутри треугольникаABC, тоAP — диагональ. Следовательно, число вершин, из которых нельзя провести диагональ, не превосходит [n/2] (т. е. целой части числаn/2). С другой стороны, существуютn-угольники, для которых эта оценка достигается (рис.).

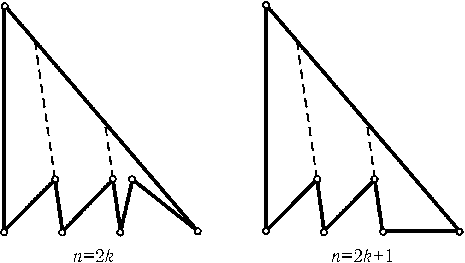
Ответ задачи отсутствует