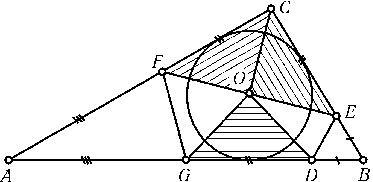
ПустьAB — наибольшая сторона треугольникаABCиAC$\ge$BC. Возьмем сначала на сторонеABточкуDтак, чтоAD=AC, затем наBC — точкуEтак, чтоBE=BD, затем наAC — точкуFтак, чтоCF=CE, затем наAB — точкуGтак, чтоAG=AF(рис.). ТогдаGD=FC=CE. ПустьO — центр вписанной окружности треугольникаABC. Так как$\angle$CAO=$\angle$DAOиCA=DA, то$\triangle$CAO=$\triangle$DAO, поэтомуOC=OD. АналогичноOF=OG,OC=OGиOD=OE. ПоэтомуOE=OD=OC=OG=OF, т. е. на рис. изображено требуемое разбиение.

Ответ задачи отсутствует