Задание олимпиады: неравенство Птолемея и вписанные многоугольники
Задача
а) Докажите, что еслиA,B,CиD — произвольные точки плоскости, тоAB . CD+BC . AD$\ge$AC . BD(неравенство Птолемея). б) Докажите, что еслиA1,A2, ...A6 — произвольные точки плоскости, то
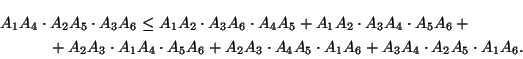
в) Докажите, что (нестрогое) неравенство Птолемея обращается в равенство тогда и только тогда, когдаABCD — (выпуклый) вписанный четырехугольник. г) Докажите, что неравенство из задачи б) обращается в равенство тогда и только тогда, когдаA1...A6 — вписанный шестиугольник.
Решение
а) Утверждение задачи вытекает из следующих свойств комплексных чисел: 1)|zw| = |z| . |w|; 2)|z+w|$\le$|z| + |w|. Действительно, еслиa,b,c,d — произвольные комплексные числа, то
(a - b)(c - d )+ (b - c)(a - d )= (a - c)(b - d ).
Поэтому
| a - b| . | c - d| + | b - c| . | a - d|$\displaystyle \ge$| a - c| . | b - d|.
б) Нужно лишь проверить соответствующее тождество для комплексных чиселa1,
...,a6(это тождество получается из написанного в условии неравенства
заменой знака$\le$на знак =, и заменой каждого сомножителяAiAjна
сомножитель (ai-aj).
в) Нестрогое неравенство|z+w|$\le$|z| + |w| обращается в равенство тогда и
только тогда, когда комплексные числаzиwпропорциональны с вещественным
положительным коэффициентом пропорциональности. Поэтому, как видно из решения
задачи а), неравенство Птолемея обращается в равенство тогда и только тогда,
когда число${\frac{(a-b)(c-d)}{(b-c)(a-d)}}$вещественно и положительно, т. е.
числоq=${\frac{a-b}{a-d}}$:${\frac{c-b}{c-d}}$вещественно и отрицательно. Числоq — это двойное отношение чиселa,b,c,d. Согласно
задаче 29.27, б) оно вещественно тогда и только тогда, когда данные
точки лежат на одной окружности. Остается доказать, что если данные точки лежат
на одной окружности, тоqотрицательно тогда и только тогда, когда ломанаяabcdнесамопересекающаяся. Последнее условие эквивалентно тому, что точкиbиdлежат на разных дугах, высекаемых точкамиaиc. Отобразим нашу
окружность при помощи инверсии на прямую. В решении задачи 29.26показано, что двойное отношение сохраняется при инверсии. Поэтому еслиa*,b*,c*,d* — комплексные числа, соответствующие образам наших
точек, то их двойное отношение равноq. Рассматривая всевозможные (с
точностью до порядка) способы расположения точекa*,b*,c*,d*на
прямой, легко убедиться, чтоq< 0 тогда и только тогда, когда на отрезкеa'c'лежит ровно одна из точекb'иd'.
г) Задачу б) можно следующим образом решить с помощью неравенства Птолемея: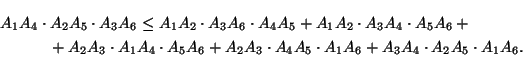
Все использованные нестрогие неравенства обращаются в равенства тогда и только тогда, когда четырехугольникиA1A2A3A4,A2A3A4A5,A1A3A5A6иA1A2A4A5вписанные. Легко видеть, что это эквивалентно тому, что шестиугольникA1...A6вписанный.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет