Задача
Вершины треугольника соответствуют комплексным числамa,bиc, лежащим на единичной окружности с центром в нуле. Докажите, что если точкиzиwизогонально сопряжены, тоz+w+abc$\bar{z}$$\bar{w}$=a+b+c(Морли).
Решение
Согласно задаче 29.20
$\displaystyle \Im$(a - z)(a - w)($\displaystyle \bar{a}$ - $\displaystyle \bar{b}$)($\displaystyle \bar{a}$ - $\displaystyle \bar{c}$) = 0.
Обозначим($\bar{a}$-$\bar{b}$)($\bar{a}$-$\bar{c}$),($\bar{b}$-$\bar{a}$)($\bar{b}$-$\bar{c}$)
и($\bar{c}$-$\bar{a}$)($\bar{c}$-$\bar{b}$) черезA,BиCсоответственно. Тогда
$\displaystyle \Im$a2A - $\displaystyle \Im$aA(z + w) + $\displaystyle \Im$Azw = 0.1)
Заметим, чтоa(b+c)A — вещественное число. Действительно,
a(b + c)A = 2$\displaystyle \Re$$\displaystyle \bigl($$\displaystyle \bar{a}$(b + c)$\displaystyle \bigr)$ - | a(b + c)|2
(чтобы проверить это равенство, нужно воспользоваться тем, что$\Re$$\zeta$= ($\zeta$+$\bar{\zeta}$)/2, и тем, чтоa$\bar{a}$=b$\bar{b}$=c$\bar{c}$= 1,
поскольку точкиa,b,cлежат на единичной окружности). Таким образом,
$\displaystyle \Im$a2A = $\displaystyle \Im$$\displaystyle \bigl($(a + b + c)aA$\displaystyle \bigr)$ - $\displaystyle \Im$$\displaystyle \bigl($a(b + c)A$\displaystyle \bigr)$ = $\displaystyle \Im$$\displaystyle \bigl($aA(a + b + c)$\displaystyle \bigr)$.
Далее,
abc . aA = ab($\displaystyle \bar{a}$ - $\displaystyle \bar{b}$) . ac($\displaystyle \bar{a}$ - $\displaystyle \bar{c}$) = (a - b)(a - c) = $\displaystyle \bar{A}$.
Следовательно,
$\displaystyle \Im$Azw = - $\displaystyle \Im$$\displaystyle \overline{Azw}$ = - $\displaystyle \Im$aA . abc . $\displaystyle \bar{z}$$\displaystyle \bar{w}$.
Подставляя эти равенства в (1), получаем
$\displaystyle \Im$aA[a + b + c - (z + w) - abc . $\displaystyle \bar{z}$$\displaystyle \bar{w}$] = $\displaystyle \Im$aAp = 0
(черезpобозначено выражение в квадратных скобках).
Аналогично доказывается, что$\Im$bBp=$\Im$cCp= 0. Таким образом, либоp= 0 и
тогда утверждение задачи доказано, либо числаaA,bBиcCпропорциональны
с вещественным коэффициентом пропорциональности. Но второй случай невозможен,
так как иначе число
$\displaystyle {\frac{aA}{bB}}$ = $\displaystyle {\frac{a}{b}}$ . $\displaystyle {\frac{\bar a-\bar c}{\bar c-\bar b}}$
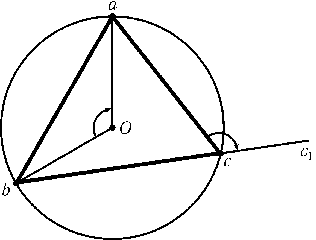
было бы вещественным, т. е.$\angle$bOa=$\angle$acc1=$\pi$n(углы
ориентированные: рис.). Однако$\angle$acc1=$\pi$-$\angle$cи$\angle$bOa= 2$\angle$cпо теореме о вписанном угле, поэтому$\angle$c=$\pi$(n- 1), чего не может быть.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет