Задача
Числовая последовательность A1, A2, ..., An, ... определена равенствами A1 = 1, A2 = – 1, An = – An–1 – 2An–2 (n ≥ 3).
Докажите, что при любом натуральном n число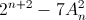 
является полным квадратом.
Решение
Решение 1: Рассмотрим другую последовательность B1, ..., Bn, ..., определенную тем же рекуррентным соотношением, но с другими начальными условиями:
B1 = 1, B2 = 3. Докажем по индукции соотношения: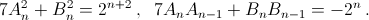 
База.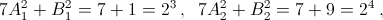 
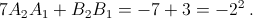
Шаг индукции.
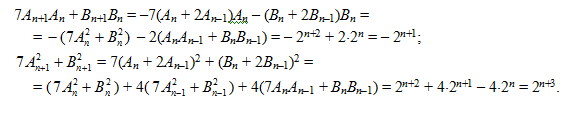
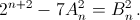
Решение 2: Не нарушая рекуррентное соотношение, добавим к последовательности член A0 = 0. Рассмотрим последовательность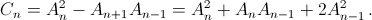 
Заметим, что 
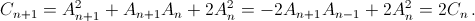Поскольку C1 = 1, отсюда следует, что Cn = 2n–1 и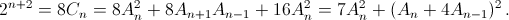 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет