Олимпиадная задача: доказательство тождеств по треугольнику Паскаля (9
Задача
Докажите тождества: а) 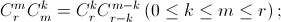 б)
б) 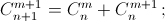 в)
в) 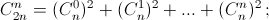 г)
г) 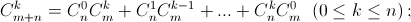 д)
д) 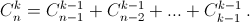 (Попробуйте доказать эти тождества тремя разными способами: пользуясь тем, что
(Попробуйте доказать эти тождества тремя разными способами: пользуясь тем, что 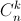 – это количество k-элементных подмножеств в множестве из n элементов; исходя из того, что
– это количество k-элементных подмножеств в множестве из n элементов; исходя из того, что 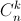 – это коэффициент при xk у многочлена (1 + x)n; пользуясь "шахматным городом" из задачи 160395).
– это коэффициент при xk у многочлена (1 + x)n; пользуясь "шахматным городом" из задачи 160395).
Решение
Решение 1:а) Пусть нам из r человек надо выбрать комиссию в составе m человек, а внутри неё – штаб из k человек. Если сначала выбрать членов комиссии, а из них выбирать штаб, то подсчёт числа способов это сделать приведёт по правилу произведения к левой части равенства. Но можно поступить по-другому: сначала выбрать штаб, а потом из оставшихся r – k человек выбрать m – k "простых" членов комиссии. Тогда подсчёт приведёт к правой части равенства. б) Пусть есть n + 1 шар: один – чёрный, а остальные – белые. Тогда число способов выбрать m + 1 белый шар равно 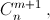 а число способов выбрать m белых и один чёрный шар равно
а число способов выбрать m белых и один чёрный шар равно 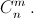 В сумме получим общее число способов выбрать m + 1 шар из n + 1, то есть
В сумме получим общее число способов выбрать m + 1 шар из n + 1, то есть 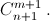 в) Достаточно в г) взять k = m = n. г) Пусть есть набор из m чёрных и n белых шаров. При каждом
p от 0 до k число способов выбрать p белых и k – p чёрных шаров равно
в) Достаточно в г) взять k = m = n. г) Пусть есть набор из m чёрных и n белых шаров. При каждом
p от 0 до k число способов выбрать p белых и k – p чёрных шаров равно 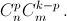 Складывая, получим общее число способов выбрать k шаров из m + n, то есть
Складывая, получим общее число способов выбрать k шаров из m + n, то есть 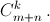 д) Пусть есть множество {a1, ..., an} из n элементов. Вместо того, чтобы сразу найти число способов выбрать из него k элементов, найдём сначала количество k-элементных множеств, содержащих a1 (их будет
д) Пусть есть множество {a1, ..., an} из n элементов. Вместо того, чтобы сразу найти число способов выбрать из него k элементов, найдём сначала количество k-элементных множеств, содержащих a1 (их будет 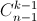 ); затем не содержащих a1, но содержащих a2
(их
); затем не содержащих a1, но содержащих a2
(их 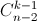 ) и так далее. В результате получим правую часть.
) и так далее. В результате получим правую часть.
Решение 2:а) Найдём двумя способами коэффициент при xm–kyk в многочлене (1 + x + y)r. Записав его в виде (1 + (x + y))r, заметим, что он равен коэффициенту при xm–kyk в многочлене 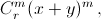 то есть
то есть 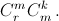 С другой стороны, записав его в виде ((1 + x) + y)r, получим, что он равен коэффициенту при при xm–kyk в многочлене
С другой стороны, записав его в виде ((1 + x) + y)r, получим, что он равен коэффициенту при при xm–kyk в многочлене 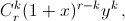 то есть
то есть 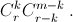 б) В равенстве (1 + x)n+1 = (1 + x)n(1 + x) одночлен
б) В равенстве (1 + x)n+1 = (1 + x)n(1 + x) одночлен 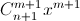 в левой части получается как сумма одночленов
в левой части получается как сумма одночленов 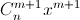 и
и 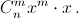 г) В равенстве (1 + x)m+n = (1 + x)n(1 + x)m одночлен
г) В равенстве (1 + x)m+n = (1 + x)n(1 + x)m одночлен 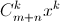 в левой части получается как сумма одночленов
в левой части получается как сумма одночленов 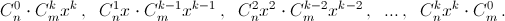 д) Перепишем формулу п. б) в виде
д) Перепишем формулу п. б) в виде 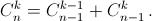 Применяя её последовательно, получим
Применяя её последовательно, получим 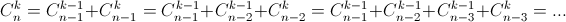 На последнем шаге надо заметить, что
На последнем шаге надо заметить, что 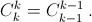
Решение 3:б) 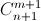 – количество путей, ведущих из вершины треугольника Паскаля к числу, стоящему на (m+1)-м месте в (n+1)-й строке. Каждый такой путь проходит либо через m-е, либо через (m+1)-е число m-й строки и в далее за один "ход" попадает в нужное место. Путей второго типа –
– количество путей, ведущих из вершины треугольника Паскаля к числу, стоящему на (m+1)-м месте в (n+1)-й строке. Каждый такой путь проходит либо через m-е, либо через (m+1)-е число m-й строки и в далее за один "ход" попадает в нужное место. Путей второго типа – 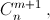 а первого –
а первого – 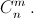 в)
в) 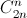 – количество путей, ведущих из вершины треугольника Паскаля к числу, стоящему на n-м месте в 2n-й строке. Каждый такой путь проходит ровно через одно число n-й строки. При этом количество путей, проходящих через число, стоящее на k-м месте, равно
– количество путей, ведущих из вершины треугольника Паскаля к числу, стоящему на n-м месте в 2n-й строке. Каждый такой путь проходит ровно через одно число n-й строки. При этом количество путей, проходящих через число, стоящее на k-м месте, равно 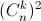 (к указанной точке ведут
(к указанной точке ведут 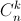 путей, а из неё до нужного места – столько же). г)
путей, а из неё до нужного места – столько же). г) 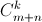 – количество путей, ведущих из вершины треугольника Паскаля к числу, стоящему на k-м месте в (m+n)-й строке. Каждый такой путь проходит ровно через одно число n-й строки. При этом количество путей, проходящих через число, стоящее на l-м месте, равно
– количество путей, ведущих из вершины треугольника Паскаля к числу, стоящему на k-м месте в (m+n)-й строке. Каждый такой путь проходит ровно через одно число n-й строки. При этом количество путей, проходящих через число, стоящее на l-м месте, равно 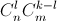 (к указанной точке ведут
(к указанной точке ведут 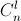 путей, а из неё до нужного места –
путей, а из неё до нужного места – 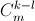 путей). д) См. задачу 130713.
путей). д) См. задачу 130713.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь