Задача
а) Пусть {a1, a2,..., an} – последовательность целых чисел, сумма которых равна 1. Докажите, что ровно у одного из ее циклических сдвигов
{a1, a2, ..., an}, {a2, ..., an, a1}, ..., {an, a1, ..., an–1} все частичные суммы (от начала до произвольного элемента) положительны. б) Выведите отсюда равенства: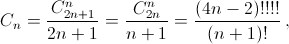 
где (4n – 2)!!!! = 2·6·10·...(4n – 2) – произведение, в котором участвует каждое четвёртое число.
Определение чисел Каталана Cn смотри в справочнике.
Решение
а) Назовем весом последовательности такое число k, что частичные суммы s1 = a1, ..., sk = a1 + ... + ak положительны, а sk+1 ≤ 0 (если k < n). Рассмотрим циклический сдвиг, после которого образуется последовательность {b1, ..., bn} наибольшего веса. Докажем, что этот вес равен n. Пусть это не так, тогда рассмотрим наиболее "длинную" неположительную частичную сумму b1 + ... + bk. Тогда все суммы bk+1, bk+1 + bk+2, ..., bk+1 + ... + bn положительны. Это значит, что переставив bk+1, ..., bn в начало последовательности, мы увеличим ее вес. Противоречие.
Пусть есть два разных циклических сдвига, удовлетворяющих условию. Например, и у {a1, a2, ..., an} и у {am, ..., an, a1, ..., am–1} все частичные суммы положительны. Тогда числа a1 + ... + am–1 и am + ... + an натуральные, а их сумма равна 1. Противоречие. б) Количество последовательностей из n + 1 единиц и n минус единиц равно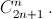 
Из а) следует, что количество таких последовательностей, у которых все частичные суммы положительны, равно 
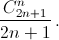Отбросив у каждой первый член (который равен 1), мы получим все последовательности из задачи 160447, а их Cn.
Последнее равенство следует из того, что (2n)! = 1·3·...·(2n – 1)·2·4·...·2n = 2·6·...·(4n – 2)·1·2·...·n = (4n – 2)!!!!·n!.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь