Задача
Пусть a0 – целое, a1, ..., an – натуральные числа. Определим две последовательности
P–1 = 1, P0 = a0, Pk = akPk–1 + Pk–2 (1 ≤ k ≤ n); Q–1 = 0, Q0 = 1, Qk = akQk–1 + Qk–2 (1 ≤ k ≤ n).
Дроби Pk/Qk называются подходящими дробями к числу [a0; a1, a2, ..., an].
Докажите, что построенные последовательности для k = 0, 1, ..., n обладают следующими свойствами:
а) Pk/Qk = [a0; a1, a2,..., ak];
б) PkQk–1 – Pk–1Qk = (–1)k+1;
в) (Pk, Qk) = 1.
Решение
а) Индукция. База. При k = 0, 1 равенство проверяется непосредственно.
Шаг индукции. Подходящая дробь с номером k + 1 получается из k-й дроби заменой ak на
ak + 
: [a0; a1, ..., ak, ak+1] = [a0; a1, ..., ak + ].
Делая такую замену в равенстве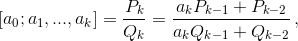 
приходим к соотношению
[a0; a1, ..., ak, ak+1] =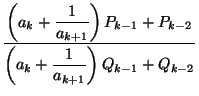 
= 
. б) Легко проверяется по индукции. в) Из б) немедленно следует, что числа Pk и Qk взаимно просты.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь