Олимпиадная задача по теории чисел: делимость для простых p
Задача
а) Докажите, что если p — простое число и 2 ≤ k ≤ p – 2, то 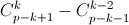 делится на p. б) Верно ли обратное утверждение?
делится на p. б) Верно ли обратное утверждение?
Решение
а) При k > p – k + 1 (2k > p + 1) оба биномиальных коэффициента равны нулю, а при 2k = p + 1 – единице. Поэтому далее считаем, что 2k ≤ p.
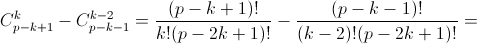
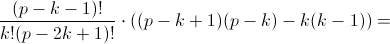
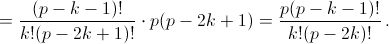
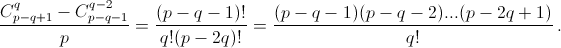
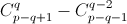 не делится наp.
не делится наp.
Ответ
б) Верно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет