Многочлен P(x) и Q(x)=P(x)·P(–x) — олимпиадная задача по математике
Задача
Пусть многочлен P(x) = xn + an–1xn–1 + ... + a1x + a0  имеет корни  x1, x2, ..., xn,  то есть  P(x) = (x – x1)(x – x2)...(x – xn).  Рассмотрим многочлен
Q(x) = P(x)P(– x).  Докажите, что
а) многочлен Q(x) имеет степень 2n и содержит только чётные степени переменной x;
б) функция Q(![]() ) является многочленом с корнями
) является многочленом с корнями 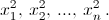
Решение
а) 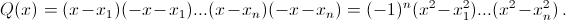 Отсюда и следует доказываемое утверждение. б) Сделав в Q(x) замену t = x², получим многочлен
Отсюда и следует доказываемое утверждение. б) Сделав в Q(x) замену t = x², получим многочлен 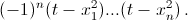 Корни этого многочлена –
Корни этого многочлена – 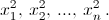
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет