Задача
Последовательность a0, a1, a2, ... задана условиями a0 = 0, an+1 = P(an) (n ≥ 0), где P(x) – многочлен с целыми коэффициентами, P(x) > 0 при x ≥ 0.
Докажите, что для любых натуральных m и k (am, ak) = a(m, k).
Решение
Пусть Q – многочлен с целыми коэффициентами, a – целое число. Тогда (Q(a), a) = (Q(0), a).
Пусть m > k. Положим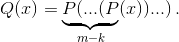 
Тогда
(am, ak) = (Q(ak), ak) = (Q(0), ak) = (am-k, ak).
Применяя алгоритм Евклида, получаем отсюда, что (am, ak) = a(m, k).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет