Задача
Упростите выражение: 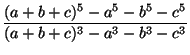 .
.
Решение
(a + b + c)3 – a3 – b3 – c3 = 3(a + b)(a + c)(b + c) (см задачу 161005 ж). Разложим на множители числитель. Первый способ. (a + b)5 – a5 – b5 = 5ab(a3 + b3) + 10a2b2(a + b) = 5ab(a + b)(a2 + ab + b2). Поэтому
(a + b + c)5 – a5 – b5 – c5 = (a + b + c)5 – (a + b)5 – c5 + (a + b)5 – a5 – b5 =
= 5c(a + b)(a + b + c)((a + b)2 + (a + b)c + c2) + 5ab(a + b)(a2 + ab + b2) =
= 5(a + b)(c(a + b + c)(a2 + b2 + c2 + 2ab + ac + bc) + ab(a2 + ab + b2)) =
= 5(a + b)(c(a + b + c)(a2 + b2 + c2 + ab + ac + bc) + abc(a + b + c) + ab(a2 + ab + b2)) =
= 5(a + b)(a2 + b2 + c2 + ab + ac + bc)·(c(a + b + c) + ab) = 5(a + b)(b + c)(a + c)(a2 + b2 + c2 + ab + ac + bc). Второй способ. По теореме Безу (см. задачу 160961) многочлен в числителе делится на a + b, a + c и b + c, а значит, и на их произведение. В частном должен получиться симметрический многочлен второй степени, то есть вида p(a2 + b2 + c2) + q(ab + ac + bc). Подставляя вместо (a, b, c) (1, 1, 0) и (2, –1, 0), найдем, что p = q = 5.
(Можно также в равенстве (a + b + c)5 – a5 – b5 – c5 = (a + b)(b + c)(a + c)(p(a2 + b2 + c2) + q(ab + ac + bc)) сравнить коэффициенты при a4b и a3b2.)
Итак, 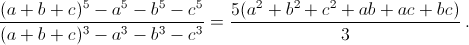 .
.
Ответ
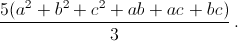
Чтобы оставлять комментарии, войдите или зарегистрируйтесь