Задача
Положительные числа a, b, c, x, y, таковы, что
x² + xy + y² = a²,
y² + yz + z² = b²,
x² + xz + z² = c².
Выразите величину xy + yz + xz через a, b и c.
Решение
Выпустим из точки O три луча с углами 120° между ними и отложим на них отрезки OA = z, OB = x, OC = y. По теореме косинусов стороны треугольника ABC равны a, b и c. При этом ½ (xy + yz + xz) sin 120° = SOBC + SOAC + SOAB = SABC, то есть 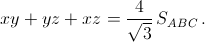
Ответ
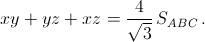 где
p = ½ (a + b + c).
где
p = ½ (a + b + c).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет