Математическая задача: метод Ньютона и приближённые корни уравнений
Задача
Метод Ньютона.Для приближенного нахождения корней уравненияf(x) = 0 Ньютон предложил искать последовательные приближения по формуле
xn + 1 = xn - 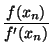 ,
,
(начальное условиеx0следует выбирать поближе к искомому корню).
Докажите, что для функцииf(x) =x2-kи начального условияx0> 0 итерационный процесс всегда будет сходиться к$\sqrt{k}$,
то есть$\lim\limits_{n\to\infty}^{}$xn=$\sqrt{k}$.
Как будет выражатьсяxn + 1черезxn? Сравните результат с
формулой из задачи 9.48.
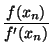 ,
,
Решение
Решение задачи отсутствует
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет