Задача
а) Докажите, что для любого многочлена f(x) степени n существует единственное представление его в виде
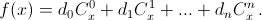
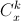интерпретируется как многочлен от переменнойx. В частности, нижний индекс у биномиального коэффициента может быть любым действительным числом.б) Докажите, что коэффициенты d0, d1, ..., dn в этом представлении вычисляются по формуле dk = Δkf(0)
(0 ≤ k ≤ n).
Решение
а) Докажем по индукции, что такое представление существует. База (n = 0) очевидна.
Шаг индукции. Поскольку многочлены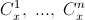 
обращаются в ноль в точке x = 0, то d0 = f(0).
При этом f(x) = d0 + xg(x). Положим t = x – 1. По предположению индукции многочлен g(t + 1) записывается в виде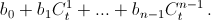 
Значит,
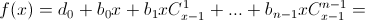
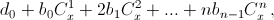
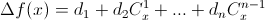(поскольку 
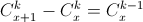). Значит, 
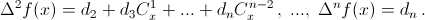Подставив в эти равенства x = 0, получаем нужное утверждение.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет