Задание олимпиады: производящая функция чисел Фибоначчи и формула Бине
Задача
Решение
а) Из равенства Fn = Fn–1 + Fn–2 получаем F(x) = F0 + (F1 – F0)x + x²F(x) = x + x²F(x), откуда 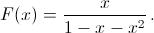
Осталось заметить, что φ и ![]() – корни уравнения x² – x – 1 = 0, то есть
– корни уравнения x² – x – 1 = 0, то есть 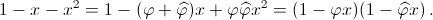 б)
б) 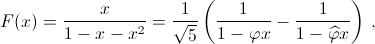
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет
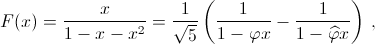 где
где