Задача
Пусть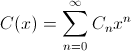 
– производящая функция последовательности чисел Каталана. Докажите, что она удовлетворяет равенству
C(x) = xC²(x) + 1,
и получите явный вид функцииC(x).
Определение чисел Каталана можно найти всправочнике.
Решение
Коэффициент при xn у функции C²(x) = (C0 + C1x + C2x² + ...)(C0 + C1x + C2x² + ...) равен C0Cn + C1Cn–1 + ... + CnC0 = Cn+1 (см. задачу 160452). Следовательно, C(x) = C0 + xC²(x) = 1 + xC²(x). Отсюда 
(Знак перед радикалом выбирается из условия C(0) = C0 = 1.)
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет