Задача
Дан треугольник ABC и такая точка F, что ∠AFB = ∠BFC = ∠CFA. Прямая, проходящая через F и перпендикулярная BC, пересекает медиану, проведённую из вершины A, в точке A1. Точки B1 и C1 определяются аналогично. Докажите, что A1, B1 и C1 являются тремя вершинами правильного шестиугольника, три другие вершины которого лежат на сторонах треугольника ABC.
Решение
Решение 1: Возьмем правильный шестиугольник A1B'C1A'B1C' и такую точку M внутри треугольника A1B1C1, что ∠B1MC1 = 180° – α, ∠C1MA1 = 180° – β,
∠A1MB1 = 180° – γ, где α, β и γ – углы треугольника ABC (эти углы меньше 120╟, потому что F лежит внутри треугольника ABC; отсюда и следует, что точка M лежит внутри треугольника A1B1C1). Пусть прямые, проходящие через A', B' и C' и перпендикулярные A1M, B1M и C1M, образуют треугольник ABC (см. рис.). Очевидно, что он подобен данному треугольнику. Значит, осталось показать, что AA1, BB1 и CC1 являются его медианами, а M – точкой Торричелли (то есть M совпадает с F).
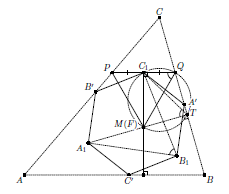
∠C1QM = ∠C1TM = ∠C1TA1 = ∠C1B1A1 = 60°. Аналогично, ∠QPM = 60°, то есть треугольник MPQ равносторонний, а C1 – середина PQ. Рассмотрев гомотетию с центром C, получаем, что CC1 – медиана, а CM проходит через третью вершину равностороннего треугольника с основанием AB и, значит, через точку Торричелли.
Решение 2: Пусть AP – первая точка Аполлония треугольник ABC (см. рис.). Её педальный треугольник A0B0C0 правильный. Точки Аполлония и Торричелли изогонально сопряжены (см. статью А.В. Акопяна и А.А. Заславского "Разные взгляды на изогональное сопряжение"). Следовательно, их педальные треугольники имеют общую описанную окружность ω (см. задачу 156954).
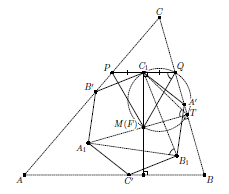
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь