Задача
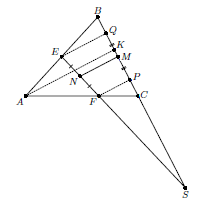
На сторонах AB и AC треугольника ABC взяты точки E и F. Прямые EF и BC пересекаются в точке S. Точки M и N – середины отрезков BC и EF соответственно. Прямая, проходящая через вершину A и параллельная MN, пересекает BC в точке K. Докажите, что BK : CK = FS : ES.
Решение
Проведём через F и E прямые, параллельные AK и пересекающие BC в точках P и Q (см. рис.). По теореме Фалеса PM = MQ, значит,
CP = BQ и 
Применив теперь теорему Менелая к треугольнику AFE и прямой CB, получим
что и требовалось доказать.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет