Решение 1:   Пусть K – вторая точка пересечения ω₁ и ω₂ (см. рис.). Достаточно показать, что  ∠OKX = 90°.

  По условию треугольники AOB и COD равнобедренные. Пусть α и β – углы при их основаниях соответственно. Тогда, по свойству вписанных углов, имеем  ∠BKC = ∠BKO + ∠CKO = ∠BAO + ∠CDO = α + β.  Учитывая, что четырёхугольник ACBD вписанный, имеем:

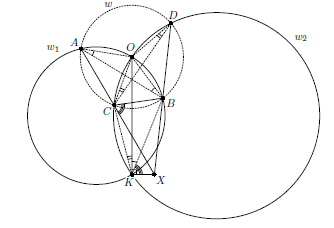
∠BCK = 180° – ∠XBC – ∠XCB = 180° – ∠CAD – ∠ADB = 180° – ½ (⌣AB + ⌣CD),  где  ⌣AB  и  ⌣CD  – дуги окружности с центром O,  ⌣AB = 180° – 2α,  ⌣CD = 180° – 2β.  Следовательно,  ∠BXC = ∠BKC,  то есть четырёхугольник BXKC вписанный. Значит,  ∠XKB = ∠XCB = 180° – ACB = 90° – α.

  Таким образом,  ∠OKX = ∠BKX + ∠BKO = 90°,  что и требовалось доказать.

  Случай, когда точки C и D меняются местами, рассматривается аналогично.

Решение 2:   Пусть OP и OQ – диаметры ω₁ и ω₂ (см. рис.). Докажем, что точка X лежат на прямой PQ.

  При инверсии относительно окружности ω окружность ω₁ перейдёт в прямую AB, а ω₂ – в CD, следовательно, точка K перейдёт в точку S пересечения AB и CD. Кроме того,  PQ ⊥ OS,  то есть PQ – поляра точки S относительно окружности ω. С другой стороны, X (как точка пересечения AC и BD) также лежит на поляре точки S. Следовательно, X принадлежит PQ.

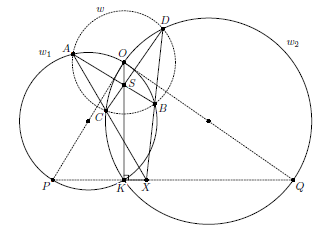
Ответ задачи отсутствует