Задача
Диагонали AC, BD трапеции ABCD пересекаются в точке P. Описанные окружности треугольников ABP, CDP пересекают прямую AD в точках X, Y. Точка M – середина XY. Докажите, что BM = CM.
Решение
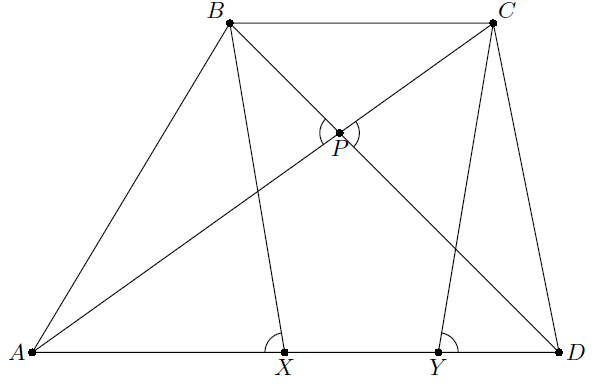
Из условия следует, что ∠BXA = ∠BPA = ∠CPD = ∠CYD (см. рис.). Значит, трапеция BXYC равнобокая, что равносильно утверждению задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет