Задачи и олимпиады по математике

Задача

В квадрате АВСD со стороной 1 точка F – середина стороны ВС, Е – основание перпендикуляра, опущенного из вершины А на DF.

Найдите длину ВЕ.

Решение

Решение 1:Продолжим отрезок DF до пересечения с прямой АВ в точке K (см. рис.). Прямоугольные треугольники KBF и DCF равны (по катету и острому углу), значит, KB = DC. Таким образом, EB – медиана прямоугольного треугольника АЕK, проведенная к гипотенузе, поэтому ВЕ = ½ AK = 1.

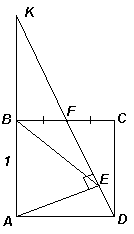
Решение 2:Так как ∠АBF = ∠AEF = 90°, то около четырёхугольника АВFE можно описать окружность, значит, ∠ВАF = ∠СFD (см. рис.).

Из равенства треугольников АВF и DCF следует, что ∠СFD = ∠ВFА. В свою очередь, ∠ВFА = ∠ВЕА. Таким образом, ∠ВАF = ∠ВEА, поэтому треугольник АВЕ – равнобедренный: ВE = АВ = 1.

Задача

Решение

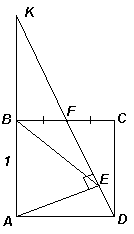
Ответ

Подтверждение удаления