Задача
На стороне CD ромба ABCD нашлась такая точка K, что AD = BK. Пусть F – точка пересечения диагонали BD и серединного перпендикуляра к стороне BC. Докажите, что точки A, F и K лежат на одной прямой.
Решение
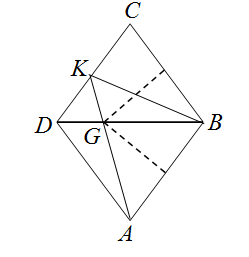
ABKD – равнобедренная трапеция (см. рис.). Точка G пересечения её диагоналей лежит на серединном перпендикуляре к основанию AB. В силу симметрии ромба ABCD относительно диагонали BD, G лежит также на серединном перпендикуляре к BC, то есть совпадает с точкой F.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет