Решение 1:   Пусть E – точка пересечения диагоналей. Достаточно рассмотреть два варианта расположения углов.

  1)  ∠BAC = ∠DAC = 55°,  ∠BCA = 19°,  ∠DCA = 16°.  Пусть I – точка пересечения биссектрис треугольника ABD. Четырёхугольник BCDI вписанный, (поскольку  ∠BID + ∠BСD = 90° + ½ ∠BAD + ∠BCA + ∠DCA = 145° + 35° = 180°).  Поэтому  ∠DBI = ∠DCI = ∠DCA = 16°.  Значит,  ∠ABD = 32°,

и  ∠AED = ∠ABD + ∠BAC = 87°.

  2)  ∠BAC = ∠BCA = 55°,  ∠DAC = 19°,  ∠DCA = 16°.  Тогда  ∠ADC = 145°,  ∠ABC = 70°.

  Рассмотрим описанную окружность треугольника ADC. Центр этой окружности является вершиной равнобедренного треугольника с основанием AC и углом при вершине, равным  2·(180° – 145°) = 70°,  то есть совпадает с точкой B. Поэтому  ∠ABD = 2 ∠DCA = 32°,  и  ∠AED = ∠ABD + ∠BAC = 87°.

Решение 2:   Рассматриваем те же варианты, что в решении 1.

  1) Имеем:  ∠ABC = 106°,  ∠ADC = 109°.  По теореме синусов 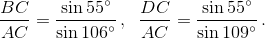    В треугольнике BCD  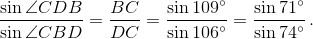    С другой стороны,  ∠CDB + ∠CAB = 180° – ∠BCD = 145° = 71° + 74°.В силу монотонности функции  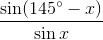   на интервале  (0°, 90°)  ∠CDB = 71°,  ∠CBD = 74°.  Следовательно, угол между диагоналями равен

71° + 16° = 87°.

  2) Так как  AB = BC,  то по теореме синусов 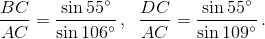    то есть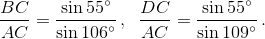  

  С другой стороны,  ∠CDB + ∠ADB = 145° = 71° + 74°.  Следовательно,  ∠CDB = 71°,  ∠ADB = 74°,  а угол между диагоналями равен

71° + 16° = 87°.

87°.