Рассмотрим одну из сумм из условия. Затем переставим в ней аргументы одного синуса и одного косинуса (назовём эти аргументы α и β, соответственно) сумма при этом изменится на

  По условию значение суммы не изменяется, значит,  sin(α – ^π/₄) = sin(β – ^π/₄).  Поскольку  α, β ∈ (0, π),  это может случиться лишь при  α – ^π/₄ = β – ^π/₄  или  α – ^π/₄ = π – (β – ^π/₄),  то есть при  β = α  или  β = ^3π/₂ – α.

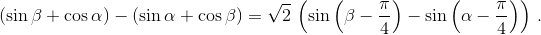
  Итак, если α – произвольный угол семиугольника, то каждый из остальных его углов равен либо α, либо ^3π/₂ – α. Значит, углы семиугольника принимают не более двух различных значений, поэтому четыре из них принимают одно и то же значение.

Ответ задачи отсутствует