Задача
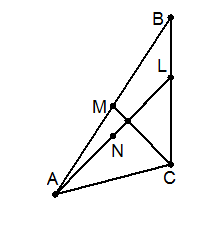
На стороне BC треугольника ABC выбрана точка L так, что AL в два раза больше медианы CM. Оказалось, что угол ALC равен 45°.
Докажите, что AL и CM перпендикулярны.
Решение
Пусть N – середина отрезка AL. Тогда MN – средняя линия треугольника BAL. Поэтому LMNC – трапеция (или параллелограмм) с равными диагоналями, то есть равнобедренная трапеция (или прямоугольник). Один из углов между её диагоналями LN и CM в два раза больше угла NLC, то есть равен 90°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет