Задача
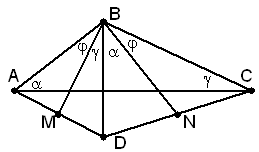
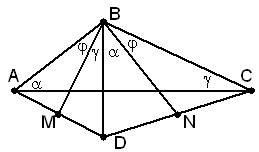
В выпуклом четырёхугольнике ABCD диагонали перпендикулярны. На сторонах AD и CD отмечены соответственно точки M и N так, что углы ABN и CBM прямые. Докажите, что прямые AC и MN параллельны.
Решение
Достаточно доказать, что AM : MD = CN : ND.
Первый способ. Заметим, что ∠BAC = ∠DBN, ∠BCA = ∠DBM, ∠ABM = ∠CBN (углы с взаимно перпендикулярными сторонами); обозначим эти углы α, β и φ.
Имеем AM : MD = SAMD : SMBD = AB sin φ : BD sin γ Аналогично CN : ND = BC sin φ : BD sin α. Осталось заметить, что AB : sin γ = BC : sin α по теореме синусов для треугольника ABC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет