Задача
Дан выпуклый четырёхугольник ABCD. Пешеход Петя выходит из вершины A, идёт по стороне AB и далее по контуру четырёхугольника. Пешеход Вася выходит из вершины A одновременно с Петей, идёт по диагонали AC и одновременно с Петей приходит в C. Пешеход Толя выходит из вершины B в тот момент, когда её проходит Петя, идёт по диагонали BD и одновременно с Петей приходит в D. Скорости пешеходов постоянны.
Могли ли Вася и Толя прийти в точку пересечения диагоналей O одновременно?
Решение
Решение 1:Пусть Петя приходит в вершину B в то же время, когда Вася проходит точку X диагонали AC, а в вершину C, когда Толя проходит точку Y диагонали BD. Тогда
AB : BC = AX : XC, BC : CD = BY : YD. Значит, BX и CY – биссектрисы углов B и C четырёхугольника. Если Вася с Толей встретились в точке O, то XO : OC = BO : OY, откуда следует параллельность прямых BX и CY. Но тогда сумма углов B и C четырёхугольника равна 2(∠XBC + ∠YCB) = 2·180° = 360°. Противоречие.
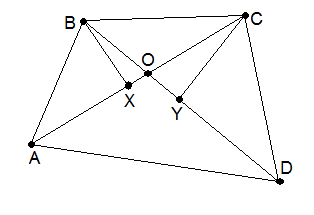
Решение 2:Рассмотрев путь от A до C (от B до D), получим, что скорость Пети больше скорости Васи (Толи). Предположим, что Вася с Толей встретились в точке O. Петя в этот момент был в некоторой точке Z стороны BC. Из неравенств скоростей следует, что BO < BZ и OC < ZC. Но тогда BO + OC < BZ + ZC = BC, что противоречит неравенству треугольника.
Ответ
Не могли.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь