а) Каждой точке X границы многоугольника соответствует "противоположная" точка X': эти две точки разбивают периметр многоугольника пополам. Следовательно, точкой X однозначно определяются прямая разбиения XX' и два многоугольника равных периметров – правый R_X (справа от луча XX') и левый L_X. То, что получаются именно многоугольники, следует из выпуклости и неравенства многоугольника.

  Занумеруем стороны многоугольника. Для каждой точки X границы пусть d_i(X) – длина куска i-й стороны, входящего в R_X (если вся сторона попала в R_X, то  d_i(X) = 0);  d₀(X) – длина отрезка XX'. Очевидно, все функции  d₀(X), d₁(X), d₂(X), ...  непрерывны. Но тогда непрерывна и функция  

d_R(X) = max {d₀(X), d₁(X), d₂(X), ...},  а это как раз длина наибольшей стороны многоугольника R_X.

  Аналогично непрерывна функция d_L(X) – длина наибольшей стороны многоугольника LX. Непрерывная функция  d_R(X) – d_L(X)  в точках A и A';  принимает противоположные значения. Поэтому найдётся точка X, в которой  d_R(X) – d_L(X) = 0,  что и требовалось.   б) Покажем, что это нельзя сделать для треугольника ABC с длинами сторон 9, 10, 11. Его полупериметр равен 15, а площадь (по формуле Герона) равна 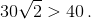    Значит, наименьшая из высот этого треугольника больше 7.

  Пусть разрез проходит через одну из вершин. Тогда длина разреза больше 7, а отрезки, на которые он делит противоположную сторону не больше

15 – 9 = 6.  Значит, они и являются наименьшими сторонами двух полученных треугольников. Но эти отрезки, очевидно, не равны.

  Пусть разрез XX' не проходит через вершину. Тогда в получившемся четырёхугольнике наименьшая сторона (пусть AX) не превосходит  (15 – 9) : 2 = 3.  Рассмотрим стороны получившегося треугольника, лежащие на сторонах исходного. Меньшая из них больше  15 – 11 = 4.  Длина разреза

XX' > AX' – AX > 7 – 3 = 4.  Итак, наименьшая сторона четырёхугольника меньше наименьшей стороны треугольника.

а) Верно;  б) неверно.