Задача
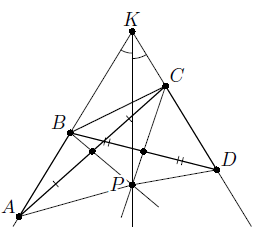
В выпуклом четырёхугольнике ABCD лучи AB и DC пересекаются в точке K. На биссектрисе угла AKD нашлась такая точка P, что прямые BP и CP делят пополам отрезки AC и BD соответственно. Докажите, что AB = CD.
Решение
Поскольку прямые BP и CP являются медианами треугольников ABC и BCD, то точки A и C равноудалены от BP, а B и D – от CP. Это значит, что
SPAB = SPBC = SPCD. С другой стороны, высоты треугольников PAB и PCD, опущенные из точки P, равны, так как P лежит на биссектрисе; значит, равны и их основания, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет