Задача
На окружности отмечены 10 точек, занумерованные по часовой стрелке: A1, A2, ..., A10, причём их можно разбить на пары симметричных относительно центра окружности. Изначально в каждой отмеченной точке сидит по кузнечику. Каждую минуту один из кузнечиков прыгает вдоль окружности через своего соседа так, чтобы расстояние между ними не изменилось. При этом нельзя пролетать над другими кузнечиками и попадать в точку, где уже сидит кузнечик. Через некоторое время оказалось, что какие-то 9 кузнечиков сидят в точках A1, A2, ..., A9, а десятый сидит на дуге A9A10A1. Можно ли утверждать, что он сидит именно в точке A10?
Решение
Десять кузнечиков разбивают окружность на 10 дуг. Покрасим эти дуги поочередно в чёрный и белый цвета (рис. слева). Изначально суммы длин чёрных и белых дуг равны, поскольку дуга, симметричная чёрной дуге относительно центра, белая, и наоборот.
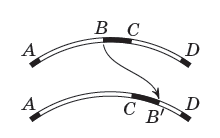
Таким образом, после каждого прыжка суммарная длина пяти дуг, взятых через одну, равна половине длины всей окружности.
Рассмотрим конечное расположение кузнечиков. Пусть десятый кузнечик находится в точке X, тогда сумма длин дуг A1A2, A3A4, A5A6, A7A8 и A9X равна половине длины окружности. Но сумма длин дуг A1A2, A3A4, A5A6, A7A8 и A9A10 также равна половине длины окружности, так как в этих точках кузнечики сидели вначале. Отсюда A9X = A9A10 и, так как обе точки X и A10 лежат на дуге A9A10A1, то точки X и A10 совпадают.
Ответ
Можно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь