Задача
Две окружности Ω1 и Ω2 с центрами O1 и O2 касаются внешним образом в точке O. Точки X и Y лежат на Ω1 и Ω2 соответственно так, что лучи O1X и O2Y одинаково направлены. Из точки X проведены касательные к Ω2, а из точки Y – к Ω1. Докажите, что эти четыре прямые касаются одной окружности, проходящей через точку O.
Решение
Обозначим через S точку пересечения XO1 и YO1 (см. рис.). Пусть r1 и r2 – радиусы соответствующих окружностей. Тогда 
. Значит, SO || O2Y и 
.
.
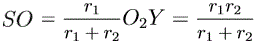Аналогично доказывается, что расстояние отSдо остальных касательных также равноSO, то естьSи есть центр требуемой окружности.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет