Задача
Девять окружностей расположены вокруг произвольного треугольника так, как показано на рисунке. Окружности, касающиеся одной и той же стороны треугольника, равны между собой. Докажите, что три прямые на рисунке пересекаются в одной точке. (Прямые проходят через вершины треугольника и центры соответствующих окружностей.)
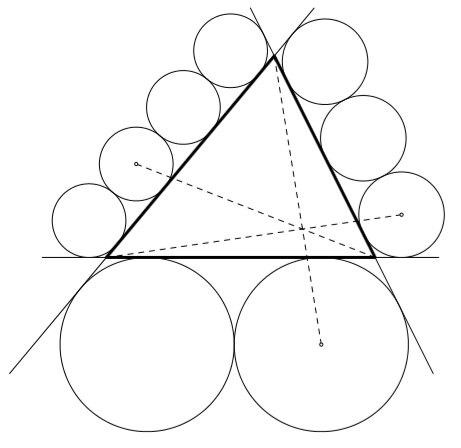
Решение
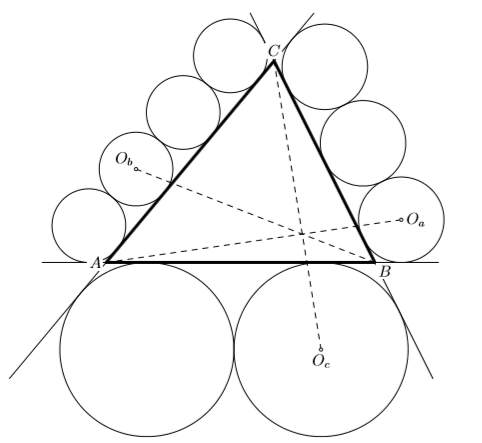
Решение 1: Введём обозначения, как на рисунке. Пусть ra, rb и rc – радиусы окружностей с центрами Oa, Ob и Oc соответственно, da(X) – расстояние от точки X до BC, db и dc определены аналогично.
Фигура, состоящая из лучей CA, CB и трёх первых, считая от C, окружностей, касающихся CA, подобна фигуре из лучей CB, CA и окружностей, касающихся CB. Следовательно, da(Ob) : rb = db(Oa) : ra. Аналогичные равенства верны для вершин A и B.
Значит,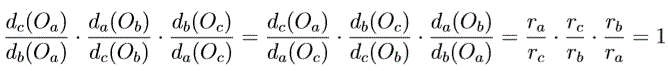 
, что по теореме Чевы влечёт утверждение задачи.
Решение 2: Пусть K, M, N – точки пересечения соответственно прямых AC и BOb, CB и AOa, CA и COc. Проведём через Ob отрезок A'C', параллельный AC (точки A' и C' расположены на прямых BA и BC соответственно). Тогда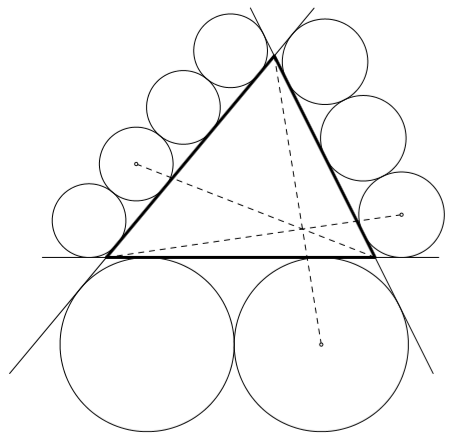 
Аналогично выразив отношения CM/BM и BN/AN, завершим решение, воспользовавшись теоремой Чевы.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь