Задача
Даны окружность, её хорда AB и середина W меньшей дуги AB. На большей дуге AB выбирается произвольная точка C. Касательная к окружности, проведённая из точки C, пересекает касательные, проведённые из точек A и B, в точках X и Y соответственно. Прямые WX и WY пересекают прямую AB в точках N и M соответственно. Докажите, что длина отрезка NM не зависит от выбора точки C.
Решение
Решение 1: Пусть отрезки AB и CW пересекаются в точке T (см. рис.). Тогда ∠ACW = ∠ABW = ∠TAW, то есть треугольники CAW и ATW подобны. Поскольку прямая WX – симедиана треугольника CAW (см. задачу 156983), она является медианой треугольника ATW, то есть точка N – середина отрезка AT. Аналогично точка M – середина BT, поэтому MN = ½ AB.
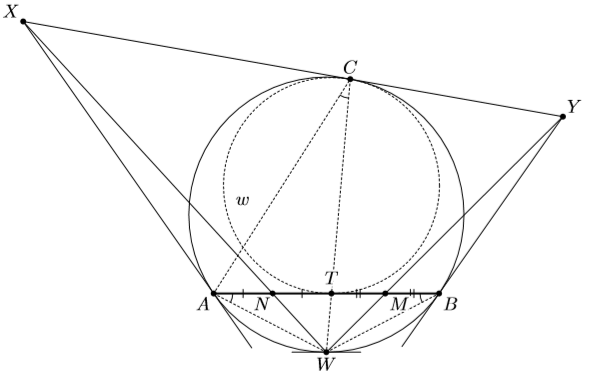
Решение 2: Поскольку W – середина дуги AB, касательная в ней параллельна AB. Совершим гомотетию с центром C, переводящую эту касательную в AB; пусть наша окружность при этой гомотетии переходит в окружность ω, а точка W – в точку T.
Из подобия треугольников CAW и ATW, доказанного в решении 1, следует, что AW² = WC·WT, то есть W лежит на радикальной оси ω и точки A. Поскольку XA = XC, точка X также на ней лежит. Значит, эта радикальная ось – прямая WX, поэтому NA² = NT², то есть N – середина AT. Аналогично M – середина BT, откуда MN = ½ AB.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь