Задача
На окружности ω c центром O фиксированы точки A и C. Точка B движется по дуге AC. Точка P – фиксированная точка хорды AC. Прямая, проходящая через P параллельно AO, пересекает прямую BA в точке A1; прямая, проходящая через P параллельно CO, пересекает прямую BC в точке C1. Докажите, что центр описанной окружности треугольника A1BC1 движется по прямой.
Решение
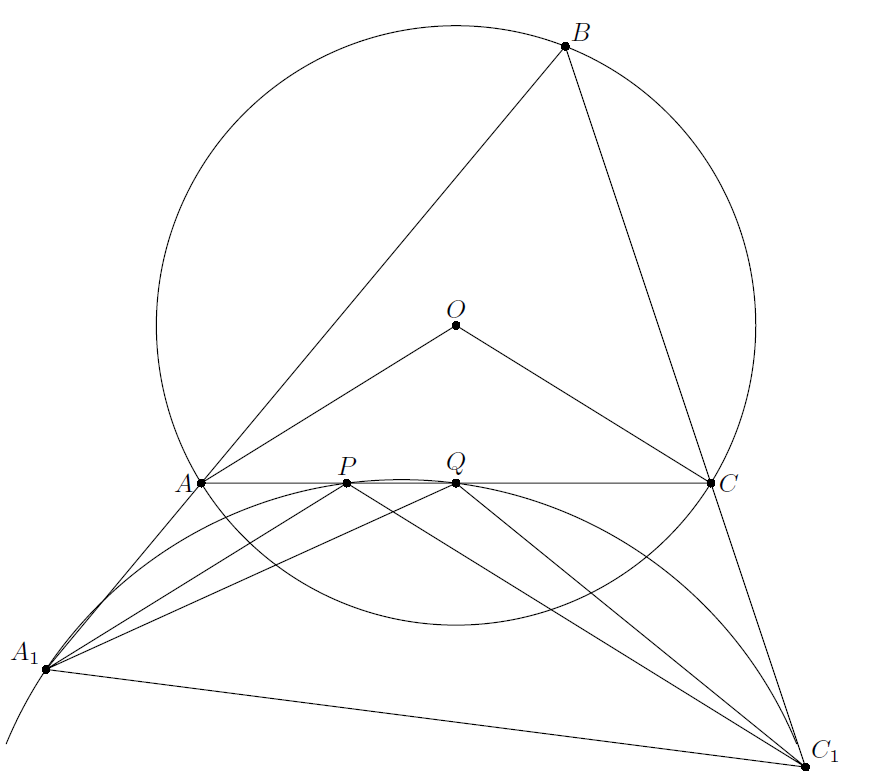
ПустьQ– вторая точка пересечения прямойACс окружностьюA1PC1. Тогда ∠QA1C1= ∠QPC1= ∠QCO= ∠QAO= ∠APA1= ∠QC1A1. Следовательно, QA1=QC1 и ∠A1QC1= ∠AOC= 2∠A1BC1, то естьQ– центр описанной окружности треугольникаA1BC1(см. рис.). Таким образом, этот центр движется по прямойAC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет