Задача
В выпуклом четырёхугольнике ABCD O – точка пересечения диагоналей, а M – середина стороны BC. Прямые MO и AD пересекаются в точке E. Докажите, что AE : ED = SABO : SCDO.
Решение
Пусть P – точка пересечения AB и MO. Применяя теорему Менелая к треугольникам ABD и ABC, получаем
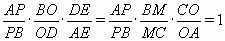. Следовательно,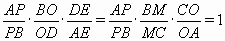 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет