Задача
Дан прямоугольный треугольник ABC. Пусть M – середина гипотенузы AB, O – центр описанной окружности ω треугольника CMB. Прямая AC вторично пересекает окружность ω в точке K. Прямая KO пересекает описанную окружность треугольника ABC в точке L. Докажите, что прямые AL и KM пересекаются на описанной окружности треугольника ACM.
Решение
Пусть прямые AL и KM пересекаются в точке N. Так как Так как BK – диаметр ω, то угол KMB – прямой и O лежит на BK. Так как AB – диаметр описанной около треугольника ABC окружности, то угол ALB – также прямой. Далее можно рассуждать по-разному. Первый способ. ∠ABL = ∠MBK = ∠MCK = ∠MCA. Угол между прямыми AL и KM равен углу ABL (углы с взаимно перпендикулярными сторонами), то есть углу MCA (см. рис.), что и требовалось.
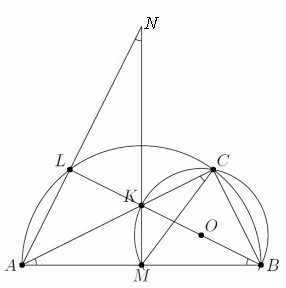
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь